
La physique est la science qui tente de modéliser les lois de la nature qui, selon Galilée, "est un livre écrit en langage mathématique". Pour valider un modèle, le physicien a besoin de prendre des mesures et vérifier qu'elles sont bien en adéquation avec le modèle proposé. Il est nécessaire pour cela de développer un système de mesure en identifiant les grandeurs à mesurer et en leur attribuant une unité pour pouvoir communiquer les résultats à d'autres physiciens. Le système d'unités actuel, appelé Système international d'unités (ou SI), repose sur une longue évolution historique de systèmes de mesures régionaux. L'importance de cette uniformisation à l'échelle planétaire du système de mesure est primordiale puisqu'elle permet une communication non ambigüe de résultats et de modèles. Un exemple célèbre est celui de la sonde Mars Climate Orbiter, lancée en 1998 pour étudier la planète Mars. Une partie du logiciel de navigation était développée par Lockheed en unités de mesures anglo-saxonnes (livres) alors que l'autre partie du logiciel était développée en unités du système métrique (newton). Cette différence a conduit à la destruction de la sonde à cause d'une correction de trajectoire erronée.
1. Grandeur et unité
1.1. Les sept grandeurs de la physique classique
Une grandeur physique est toute propriété d'un phénomène, d'un corps ou d'une substance, que l'on peut exprimer quantitativement sous forme d'un nombre et d'une référence. (Elle s'accompagne généralement d'une unité de mesure.)
Une unité de mesure est un étalon nécessaire pour la mesure d'une grandeur physique.
Historiquement, les unités étaient définies localement par les autorités d'une région. Afin de garantir une unité stable dans les échanges commerciaux, l'Assemblée nationale constituante de 1790 se prononce pour la création d'un système de mesures uniforme et simple. Cette période voit alors la naissance d'une multitude d'unités physiques (mètre, kilogramme,etc) et monétaires (franc germinal). Ces unités sont établies à l'aide d'étalons comme le mètre qui est décliné en \(4\) étalons de platine conservés aux Archives nationales de France puis recopiées sur les places de marché pour faciliter son utilisation.
Le système international (SI) s'inspire du système métrique, développé en France sous la Révolution. Il s'étend à l'Europe au cours du \(\mathrm{XIX^{e}}\) siècle et représente aujourd'hui le système de mesures le plus largement répandu sur le globe. En \(2008\), seuls trois pays dans le monde n'ont pas officiellement adopté le système international : les États-Unis, le Liberia et la Birmanie. En physique classique, on peut distinguer sept grandeurs de base, indépendantes, sur lesquelles sont basées toutes les autres grandeurs. On associe à chacune de ces grandeurs une dimension et une unité. La dernière définition des différentes unités du système international date de la conférence générale des poids et mesures qui a eu lieu en novembre 2018 (application à partir du \(20\) mai \(2019\)). Les sept grandeurs indépendantes du système international et leur définition sont répertoriées dans le tableau suivant :
| Grandeur | Dimension | Unité | Description |
|---|---|---|---|
| Longueur | L | Mètre (m) | La première définition du mètre date de la Révolution française (1791). Le mètre était défini comme "la mesure de longueur égale à la dix-millionième partie de l'arc de méridien compris entre le pôle boréal et l'équateur". Auparavant, le mètre correspondait à la longueur d'un pendule battant la seconde. Depuis le 20 mai 2019, le mètre est défini comme "la longueur du trajet parcouru dans le vide par la lumière pendant une durée de \( 1/299 792 458 \) de seconde. |
| Masse | M | Kilogramme (kg) | À l'origine, le kilogramme est défini comme la masse d'un litre d'eau ( \(1\ \mathrm{dm} ^3\) ) à \(4\) °C. Depuis le 20 mai 2019, le kilogramme est défini par la masse du prototype international, conservé au Bureau international des poids et mesures à Sèvres, en France. |
| Temps,durée | T | Secondes (s) | La seconde est originellement définie comme la durée d'un jour terrestre divisé en \(24\) heures de \(60\) minutes, elles-mêmes séparées en \(60\) secondes. Depuis le 20 mai 2019, la seconde est définie à partir d'une transition d'états atomiques de l'atome de césium 133. |
| Courant électrique | I | Ampère (A) | Historiquement, l'ampère (en hommage au physicien français André-Marie Ampère) est défini comme « l'intensité d'un courant constant qui, maintenu dans deux conducteurs parallèles, rectilignes, de longueur infinie, de section circulaire négligeable et placés à une distance de un mètre l'un de l'autre dans le vide produirait entre ces conducteurs une force égale à \(2\ \times 10^{−7}\) newton par mètre de longueur ». Depuis le 20 mai 2019, l'ampère est défini à partir de la charge élémentaire \(e=1,602\ 176\ 634\times 10^{-19} \)A.s, la seconde étant définie plus haut. |
| Température | \( \Theta \) | Kelvin (K) | Le kelvin est construit de telle sorte qu'une unité corresponde à "la fraction \(1/273,16\) de la température thermodynamique du point triple de l'eau. Depuis le 20 mai 2019, le kelvin est défini à partir de la constante de Boltzmann. |
| Quantité de matière | N | mole (mol) | Historiquement, une mole représente le nombre d'entités contenues dans \(12\) g de carbone \(12\). Aujourd'hui "une mole contient exactement \( 6,022\ 140\ 76 \times 10^{23} \) entités élémentaires. Ce nombre, appelé "nombre d’Avogadro", correspond à la valeur numérique fixée de la constante d’Avogadro, \(\mathcal{N}_A \), lorsqu’elle est exprimée en \( \mathrm{mol}^{-1}\)". |
| Intensité lumineuse | J | Candela (Cd) | La candela est l'unité de mesure de l'intensité lumineuse. |
1.2. Une multitude d'unités
Il existe en physique une multitude d'autres grandeurs que les sept énoncées précédemment. Elles ont néanmoins la propriété de toutes pouvoir se décomposer suivant les sept grandeurs indépendantes du système international.
- Une surface correspond à une longueur au carré, on dit qu'une surface est homogène à une longueur au carré (notée \( \mathrm{L^2}\)).
- Une fréquence est homogène à l'inverse d'un temps ( \( \mathrm{1/T} \), noté plus souvent \( \mathrm{T^{-1}} \))
À chaque grandeur physique \( \mathrm{X} \) mesurée est associée une et une seule dimension (notée \( \mathrm{[X]} \)) ! En revanche, une grandeur mesurée peut être exprimée avec différentes unités car plusieurs unités peuvent avoir la même dimension.
| Un volume d'eau peut être mesuré en mètres cubes (m\(^3\)) ou bien en litres (L). Cette particularité vient du fait que les litres et les mètres cubes sont tous les deux homogènes à une longueur au cube (L\(^3\)). Il faut toutefois opérer une conversion entre deux unités, ici \(1000\) L \(= 1\) m \(^3\). |

|
Ainsi, on pourra dire qu'un volume de \( 1000 \) L est strictement égal à un volume de \(1\) m\(^3\).
Un multiple (resp. sous-multiple) d'une unité de mesure est obtenue en multipliant une unité de mesure donnée par un entier supérieur (resp.inférieur) à un.
- Le mètre (m) est l'unité principale du système international permettant de mesurer une longueur. Il est décliné en plusieurs multiples (décamètre (dam), hectomètre (hm), kilomètre (km)) et sous-multiples (décimètre (dm), centimètre (cm), millimètre (mm)) suivant les préfixes et facteurs énoncés dans le cours \( \textit{MP1 : Écriture scientifique} \).
Un tableau répertoriant une liste de grandeurs et d'unités couramment utilisées est proposé ci-dessous :
| Grandeur \(X\) | Unité | Dimension \( \mathrm{[X]}\) | Décomposition en unité SI |
|---|---|---|---|
| Angle | radian (rad) ou degré (°) | // | // |
| Fréquence | Hertz (Hz) | \( \mathrm{T^{-1}} \) | \( \mathrm{s^{-1}} \) |
| Volume | Litres (L) | \( \mathrm{L^{3}} \) | \( \mathrm{m^{3}} \) |
| Force | Newton (N) | \( \mathrm{M \cdot L \cdot T^{-2}} \) | \( \mathrm{kg \cdot m \cdot s^{-2}} \) |
| Pression | Pascal (Pa) | \( \mathrm{M \cdot L^{-1} \cdot T^{-2}} \) | \( \mathrm{kg \cdot m^{-1} \cdot s^{-2} }\) |
| Puissance | Watt (W) | \( \mathrm{M \cdot L^2 \cdot T^{-3} }\) | \( \mathrm{kg \cdot m^2 \cdot s^{-3}} \) |
| Énergie | Joule (J) | \( \mathrm{M \cdot L^2 \cdot T^{-2}} \) | \( \mathrm{kg \cdot m^2 \cdot s^{-2}} \) |
| Charge électrique | Coulomb (C) | \( \mathrm{I \cdot T^{-1}} \) | \( \mathrm{A \cdot s^{-1}} \) |
| Capacité électrique | Farad (F) | \( \mathrm{T^4 \cdot I^2 \cdot M^{-1} \cdot L^{-2}} \) | \( \mathrm{s^{4} \cdot A^2 \cdot kg^{-1} \cdot m^{-2}} \) |
| Potentiel électrique | Volt (V) | \( \mathrm{L^2 \cdot M \cdot I^{-1} \cdot T^{-3}} \) | \( \mathrm{kg \cdot m^2 \cdot A^{-1} \cdot s^{-3}} \) |
1.3. Analyse dimensionnelle
Chaque calcul en physique doit être vérifié par ce que l'on appelle une étude d'homogénéité (ou analyse dimensionnelle ). Cette étude consiste à détailler la dimension de chaque terme intervenant dans un calcul dans une équation aux grandeurs et de comparer la dimension résultant de la l'opération de part et d'autre du signe "" \(=\) "".
- Écrire l'expression mathématique de la vitesse \(v = \frac{d}{t}\).
- Remplacer les variables \(d\) et \(t\) par leur grandeur \(L\) (longueur) et \(T\) (durée). Une vitesse est donc homogène à une longueur divisée par une durée \( \mathrm{[v]=L/T=L.T^{-1}} \).
- Vérifier que l'unité correspondante correspond bien à celle attendue, ici des \(\mathrm{m.s^{-1}}\).
2. Mesure physique
2.1. Précision d'une mesure
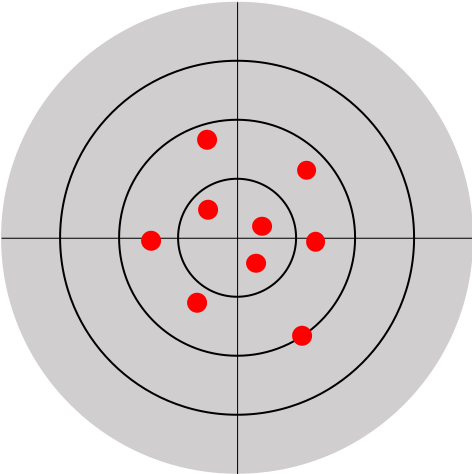
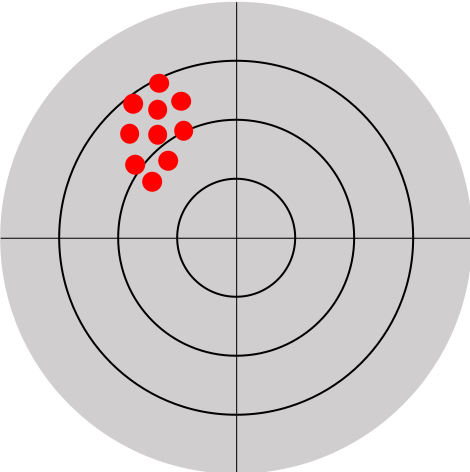
Effectuer une mesure physique consiste à utiliser un outil de mesure pour évaluer une grandeur physique. La précision d'une mesure est caractérisée par la fidélité et la justesse qui déterminent l'exactitude d'une mesure.
 |
 |
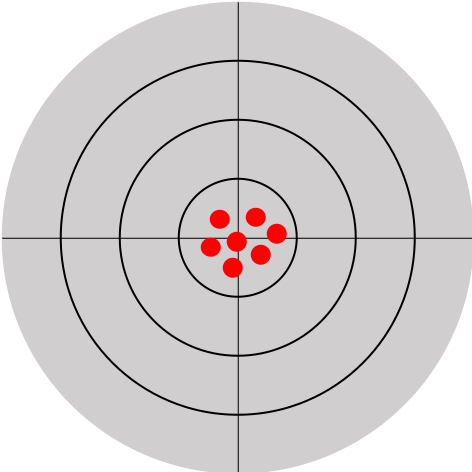 |
| (a) Série de mesures juste | (b) Série de mesures fidèle | (c) Série de mesures exacte (juste et fidèle) |
2.2. Type d'erreur
 Une mesure physique ne peut pas être exacte.
Il existe toujours une erreur qui conduit à un résultat plus ou moins proche de la valeur vraie (valeur hypothétique).
On peut distinguer deux types d'erreurs :
Une mesure physique ne peut pas être exacte.
Il existe toujours une erreur qui conduit à un résultat plus ou moins proche de la valeur vraie (valeur hypothétique).
On peut distinguer deux types d'erreurs :
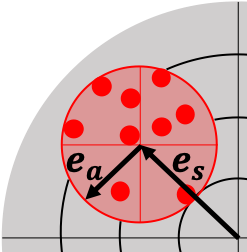
- Les erreurs aléatoires \(e_a\), obtenues lorsqu'on réalise un grand nombre de mesures. Cette erreur peut être liée aux conditions opératoires, à l'opérateur ou à la variabilité d'un paramètre physique perturbé par un grand nombre d'autres paramètres. Plus une erreur aléatoire est petite, plus la fidélité de la mesure est grande.
- Les erreurs systématiques \(e_s\) sont liées à l'appareil de mesure et peuvent être facilement compensées par un réglage. Plus l'erreur systématique est réduite, plus l'outil de mesure sera juste.
2.3. Les incertitudes associées à une mesure physique
Une mesure physique étant entachée d'erreurs, il est nécessaire de définir un intervalle dans lequel la valeur vraie se situe compte tenu de la mesure faite. Pour cela, chaque résultat d'une mesure physique est accompagné d'une incertitude.
- \( X\) est la valeur mesurée
- \( \Delta X \) est l'incertitude associée
- USI est l'unité de la mesure, préférentiellement exprimée dans le système international d'unités.
Les incertitudes de mesures sont séparées en deux catégories :
- Les incertitudes statistiques liées à des phénomènes aléatoires sont des incertitudes de type A.
- Les incertitudes de mesures liées à la précision de l'outil de mesure sont des incertitudes de type B.

