
Le principe d'inertie est l'un des principes fondamentaux de la mécanique classique. Il a été énoncé par Newton dans son ouvrage Philisophiae naturalis principia mathematica en 1687.
Le \(\mathrm{XVII}^{\textrm{ème}}\) siècle voit l'émergence de toute une théorie basée sur le mouvement des astres. Les progrès dans la mécanique sont concomitants avec les progrès techniques réalisés en optique :
- Nicolas Copernic publie sa théorie de l'héliocentrisme (1543) qui remet en cause dix-neuf siècles de conception Aristotélicienne du géocentrisme.
- L'astronome Johannes Kepler énonce, en s'appuyant sur les travaux de N. Copernic, trois lois qui permettent de décrire le mouvement des planètes (1609-1619).
- Galilée met au point sa lunette astronomique et découvre les satellites de Jupiter (1610), remettant une fois de plus en cause la théorie du géocentrisme.
- Galilée étudie le mouvement du pendule et le mouvement de chute libre puis énonce le principe de relativité (1632) qui permet de comparer les expériences dans deux référentiels différents.
- René Descartes publie les lois de la réflexion et de la réfraction, étape cruciale dans la compréhension des phénomènes d'optique.
- Isaac Newton étudie la décomposition de la lumière blanche dans un prisme et propose une interprétation corpusculaire des phénomènes lumineux.
- Le physicien Christian Huygens découvre un satellite de Saturne (Titan) et propose une interprétation ondulatoire des phénomènes lumineux (1677).
- Isaac Newton publie ses trois lois qui permettent de décrire le mouvement de n'importe quel corps (1687) :
- Le principe d'inertie (ou première loi de Newton)
- Le principe fondamental de la dynamique (ou deuxième loi de Newton)
- Le principe des actions réciproques (ou troisième loi de Newton)
1. Énoncé de la première loi de Newton
Tout corps isolé ou soumis à des forces qui se compensent persévère dans son état de repos ou de mouvement rectiligne uniforme.
2. Description du problème
2.1. Le mouvement du système
Le mouvement d'un corps, s'il n'est pas restreint à un système ponctuel, n'est pas forcément simple à étudier. Dans le cas de solides indéformables, le mouvement peut être de deux natures :
- Une translation s'il existe deux points \(A\) et \(B\) du solide tels que le vecteur \(\overrightarrow{AB}\) reste constant au cours du mouvement.
- Une rotation si la trajectoire de deux points \(A\) et \(B\) est circulaire autour d'un axe \((\Delta)\) fixe dans le référentiel d'étude.
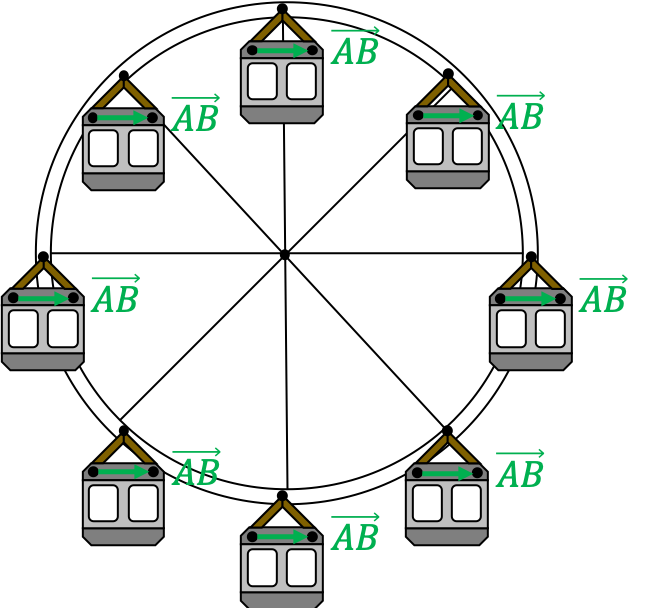 |
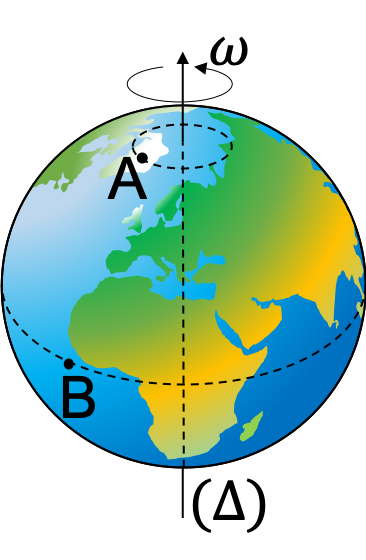 |
| (a) Translation circulaire de la cabine | (b) Rotation de la Terre autour d'un axe |
Le mouvement de rotation d'un pendule autour de son point d'attache peut être vu comme une rotation du pendule autour de son barycentre accompagné d'une translation du poids de manière à maintenir la corde tendue.
Le principe d'inertie s'intéresse en fait à la trajectoire du barycentre et non à la nature du mouvement (rotation, ou translation). Il est important de comprendre que le mouvement d'un corps peut être résumé par l'intégralité des trajectoires de tous les points qui le composent. Néanmoins, seule la trajectoire de son barycentre sera pertinente pour en déduire des informations sur les efforts auxquels est soumis ce corps.
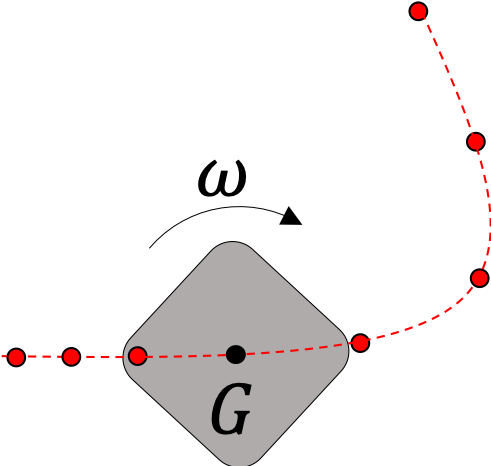
Ainsi, parmi les quatre mouvements représentés dans la figure ci-après, seuls deux mouvements sont rectilignes uniformes ((a) et (d)).
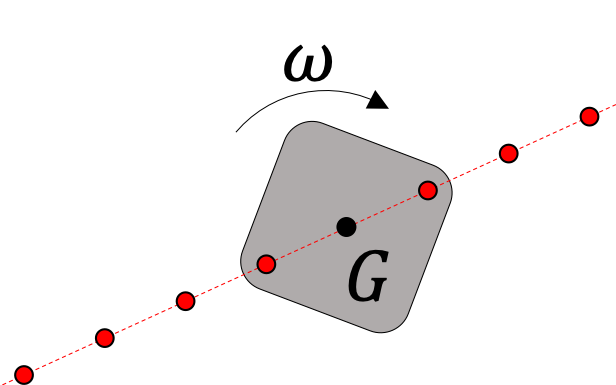 |
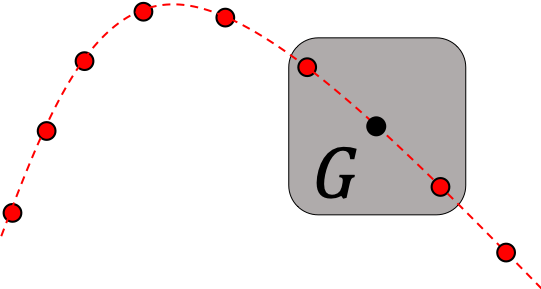 |
 |
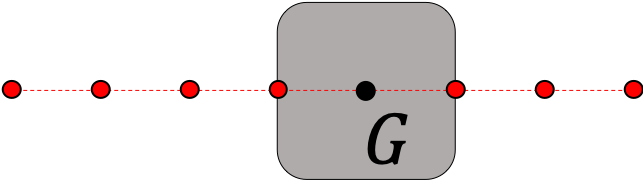 |
| (a) Mouvement de rotation. Trajectoire rectiligne uniforme du barycentre. | (b) Mouvement de translation curviligne uniforme. | (c) Mouvement de rotation. Trajectoire curviligne accélérée du barycentre. | (d) Mouvement de translation rectiligne uniforme. |
2.2. Les actions mécaniques agissant sur le système
Les actions mécaniques qui s'exercent sur un corps peuvent être de contact ou à distance. Ce qui importe, c'est que la résultante des forces soit nulle.
On dit qu'un système est isolé lorsqu'il n'est soumis à aucune action mécanique extérieure (acune force ni aucun couple).
La résultante des forces est la somme vectorielle de toutes les forces qui s'exercent sur un corps, que ces forces soient ponctuelles, surfaciques ou volumiques.
Ainsi, parmi les quatres corps représentés ci-après, trois sont soumis à des efforts qui se compensent, même s'il existe des forces non nulles qui s'exercent sur le corps.
| L'avion dans les airs | Le navire en mer |
|---|---|
|
Un avion en vol subit plusieurs forces. En rythme de croisière il est soumis à quatre forces : 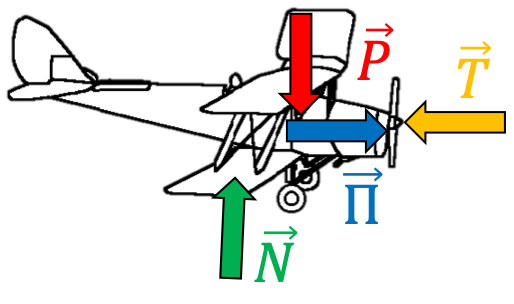
Si son altitude est maintenue constante, ainsi que sa vitesse, alors ces quatre forces se compensent. $$\large \boxed{\overrightarrow{\Pi}+\overrightarrow{P}+\overrightarrow{T}+\overrightarrow{N}=\overrightarrow{0}}$$ |
Un bateau qui navigue sur mer calme subit principalement quatre forces : 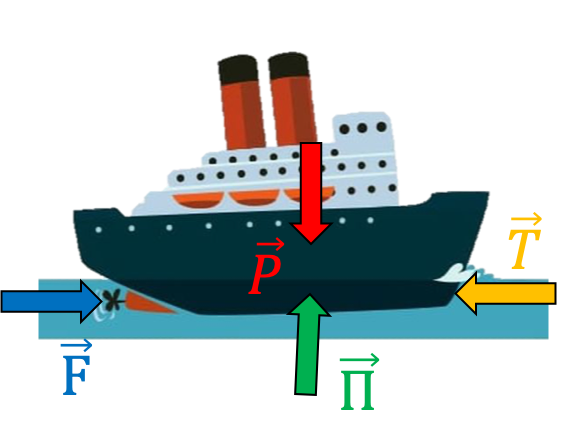
En mer calme, à vitesse constante, ces quatre forces se compensent. $$\large \boxed{\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{\Pi}=\overrightarrow{0}}$$ |
| La boule sur le sol | Le pendule |
|
Lorsqu’une boule est posée de façon immobile sur le sol, elle subit deux forces : 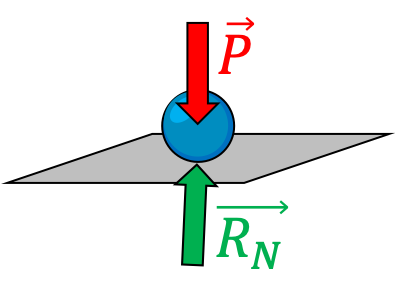
Ces deux forces se compensent exactement conformément à la troisième loi de Newton. $$\large \boxed{\overrightarrow{P}+\overrightarrow{R}_N=\overrightarrow{0}}$$ |
Le poids d’un pendule est principalement soumis à deux forces : 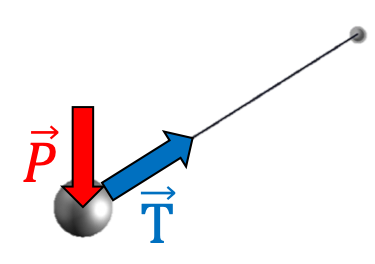
$$\large \boxed{\overrightarrow{P}+\overrightarrow{T}\neq \overrightarrow{0}}$$ |
Le principe d'inertie établit une équivalence entre un mouvement du corps et une caractéristique des forces qui s'appliquent sur lui : $$\large \boxed{\textrm{Barycentre du système en M.R.U.}} \Leftrightarrow \boxed{\textrm{Résultante des forces nulle.}}$$
3. Vers la notion de référentiel inertiel
Le principe d'inertie fait intervenir la notion de mouvement rectiligne uniforme (M.R.U.) d'un corps. Étant donné que ces corps, soumis à des forces qui se compensent, conservent leur mouvement au cours du temps, il peut être intéressant de les utiliser comme référentiels pour réaliser l'étude de phénomènes physiques. Le référentiel en translation ainsi formé par le corps en mouvement rectiligne uniforme par rapport à un référentiel de référence est dit "galiléen" (ou inertiel). Tout le problème repose désormais sur l'identification de ce "référentiel de référence" sans lequel il est impossible de trouver un référentiel inertiel.
Les lois de la physique sont les mêmes dans deux référentiels en mouvement de translation rectiligne uniforme.
Une expérience qui permet d'illustrer le principe de relativité est celle du boulet de canon lâché depuis le haut du mât d'un bateau.
| Expérience avec le bateau immobile. |
|---|
|
Un boulet de canon est lâché du haut du mât d’un bateau parfaitement immobile par rapport au rivage. Le boulet s’écrase sur le pont parfaitement à la verticale de la position où il a été lâché. On peut repérer la position du boulet dans l’espace : \(M(x,y)\). 
|
| Bateau en mouvement : interprétation de Galilée. |
|---|
|
Le même boulet est lâché du mât du bateau qui se déplace en ligne droite et à vitesse constante par rapport au rivage. Selon Galilée, la chute du boulet reste inchangée et son point d’impact sera le même que dans la première situation. 
|
| Bateau en mouvement : interprétation d'Aristote. |
|---|
|
Le même boulet est lâché du mât du bateau qui se déplace en ligne droite et à vitesse constante par rapport au rivage. Selon Aristote, le déplacement du bateau engendre une trajectoire courbée du boulet. Le point d’impact se retrouve alors « derrière » le mât. 
|

- Le référentiel du bateau noté \(\mathcal{R}\), muni du repère \((P,\overrightarrow{i}, \overrightarrow{j})\)
- Le référentiel du rivage noté \(\mathcal{R}_0\), muni du repère \((O,\overrightarrow{i}, \overrightarrow{j})\)
On repère ainsi la position du boulet avec deux vecteurs position :
- Dans le référentiel du bateau : \(\overrightarrow{PM}=x \ \overrightarrow{i}+y \ \overrightarrow{j}\)
- Dans le référentiel du rivage noté \(\overrightarrow{OM}=x' \ \overrightarrow{i}+y' \ \overrightarrow{j}\)