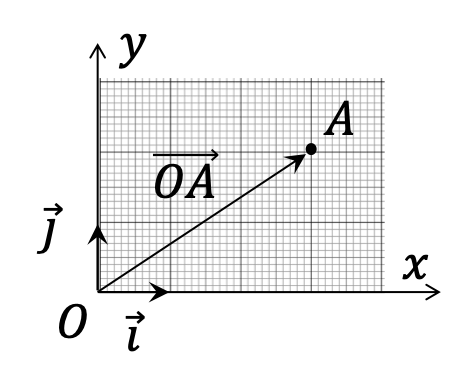La cinématique est la science qui étudie le mouvement des objets. Elle ne cherche pas à relier le mouvement à ses causes. Par conséquent, très peu d'outils sont nécessaires à l'étude du mouvement d'un corps (ou objet). Les grandeurs qui sont associées à cette étude (position, vitesse, accélération, quantité de mouvement, etc) sont appelées "grandeurs cinématiques". Ces grandeurs sont facilement représentées à l'aide de vecteurs. Afin de décrire les caractéristiques du mouvement, il est nécessaire de faire une étude préalable du cadre d'observation (système d'étude, référentiel), puis d'associer au mouvement les grandeurs cinématiques caractérisant sa trajectoire.
1. Le cadre d'étude
1.1. Le système
En mécanique, un système est un volume de l'espace (ou objet) dont on étudie le mouvement.
Dans le jeu Angry Birds®, on étudie le mouvement d'un oiseau catapulté. Dans cette situation, le système étudié est donc l'oiseau.
Cependant, afin de simplifier l'étude de son mouvement, il est commun de ne repérer qu'un point matériel en lieu et place du corps entier du volatile. L'étude se ramène ainsi à décrire le mouvement d'un point et non plus d'un objet entier. On peut donc résumer cette modélisation dans le tableau récapitulatif ci-après.
Le point matériel qui représente le système étudié est généralement noté \(M\). Il s'agit dans la majeure partie des cas d'étude du centre de gravité de l'objet, bien que rien n'empêche de choisir un autre point dont le mouvement serait plus simple à étudier.
| Système mécanique réel | Modèle du point matériel |
|---|---|
 |
 |
La réduction d'un système complexe à un seul point matériel n'est pas sans conséquence : ce processus entraîne une certaine perte d'information sur le mouvement du système étudié. Ainsi, les rotations du système ne seront plus accessibles, seules les translations pourront être décrites.
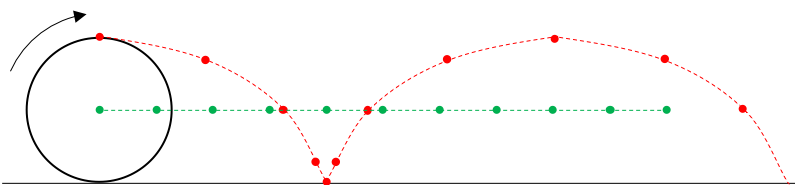
La figure suivante représente la rotation d'une roue de vélo.
On s'aperçoit que le mouvement du point vert est plus simple à décrire que le mouvement du point rouge. Cette particularité est liée au mouvement de rotation de la roue.- Dans un mouvement de translation, tous les points d'un solide ont le même mouvement.
- Dans un mouvement de rotation, tous les points d'un solide n'ont pas le même mouvement.
1.2. Le référentiel : une échelle de temps et d'espace
Un référentiel est un solide par rapport auquel on étudie le mouvement d'un système. Il est doté d'une échelle de temps (horloge) et d'espace (repère).
Ainsi, un même mouvement peut être caractérisé par rapport à plusieurs référentiels différents. Un exemple bien illustré est celui de la scène d'accrochage du film Interstellar. Le mouvement du vaisseau spatial tournant est vu par la caméra de trois points de vue différents :
- Du référentiel de Cooper et Amelia qui se situent dans un vaisseau spatial voisin.
- Du référentiel du vaisseau spatial tournant lui-même. Le référentiel d'étude est donc celui du système étudié, on parle alors de référentiel propre.
- Du référentiel de la planète environnante, qui permet de voir le mouvement relatif des deux vaisseaux spatiaux.
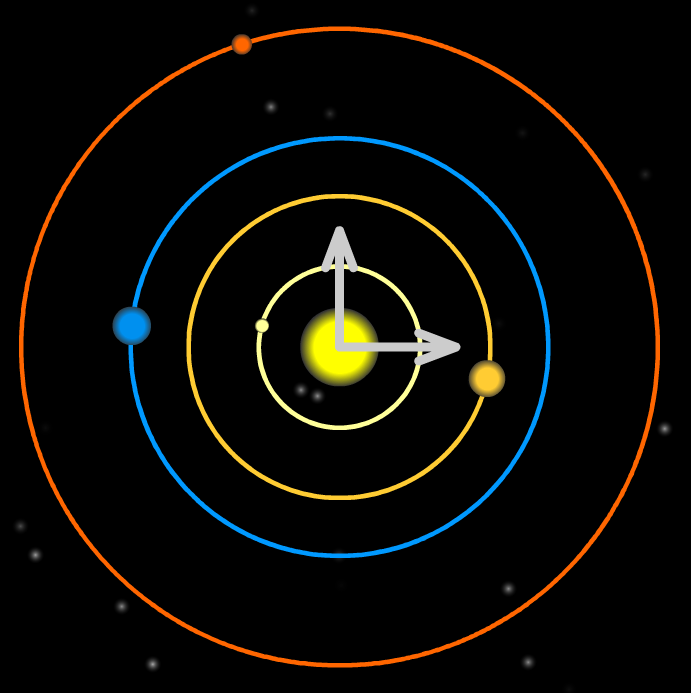
Le mouvement des planètes du système solaire peut être décrit de plusieurs points de vue différents. La représentation habituelle du mouvement des planètes se fait dans le référentiel héliocentrique, c'est-à-dire que le centre de gravité du Soleil est l'origine du repère d'étude. Dans ce référentiel, le mouvement des planètes peut s'approximer par des cercles concentriques en fonction de l'éloignement des planètes avec le Soleil (fig. 4.a).
 |
 |
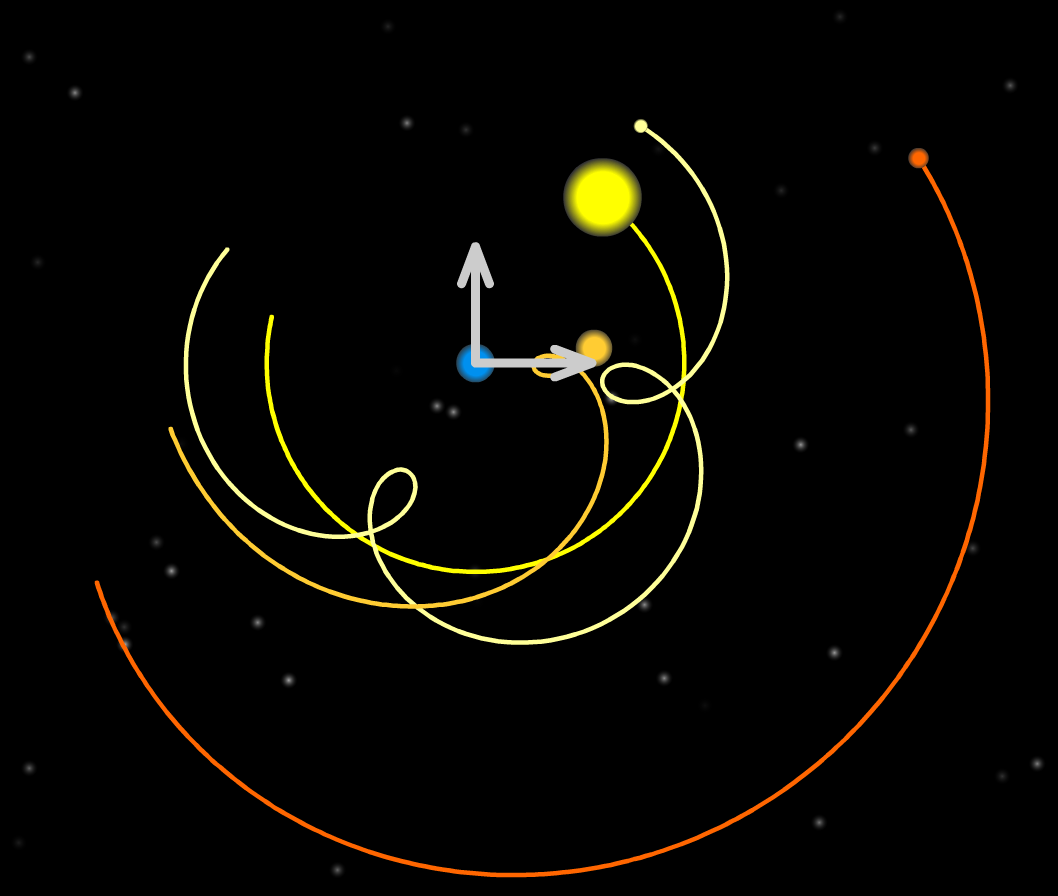 |
| (a) Référentiel héliocentrique | (b) Rétrogradation de Mars | (c) Référentiel géocentrique |
Le fait de changer de référentiel d'étude en choisissant le référentiel géocentrique, c'est-à-dire dont le centre de gravité de la Terre est l'origine du repère, permet de faire apparaître ce mouvement de rétrogradation des planètes. Le mouvement n'a pas changé, les planètes continuent de tourner autour du Soleil, mais le changement de point de vue permet d'expliquer un phénomène observé sur Terre mais difficilement représentable avec une étude dans le référentiel héliocentrique.
1.3. Rappel sur les vecteurs
Au niveau lycée, du point de vue mathématique, un vecteur est représenté par un segment orienté (une flèche), ayant pour extrémités un point de départ et un point d'arrivée. Ils sont particulièrement utiles en physique pour décrire les grandeurs cinématiques permettant de caractériser un mouvement.
Le vecteur qui va de l'origine \(O\) du repère à un point \(A\) se note \(\overrightarrow{OA}\).
Une étude de mouvement en mécanique se fait à l'aide d'un repère muni d'une origine, que l'on représente généralement par un point nommé "\(O\)", et d'une base orthonormée directe, que l'on représente à l'aide de deux ou trois vecteurs suivant que l'étude se fait en deux dimensions (mouvement plan) ou en trois dimensions. La base orthonormée directe est représentée à l'aide de deux ou trois vecteurs \(\overrightarrow{i}\) (ou \(\overrightarrow{u}_x\)), \(\overrightarrow{j}\) (ou \(\overrightarrow{u}_y\)) et \(\overrightarrow{k}\) (ou \(\overrightarrow{u}_z\)) orthogonaux et de norme unitaire. Dans le repère orthonormé direct (\(O, \overrightarrow{i}, \overrightarrow{j}\)), la représentation du vecteur \(\overrightarrow{OA}\) est donnée ci-dessous.
Il est possible de décomposer le vecteur en coordonnées qui font apparaître les composantes selon chaque direction de la base orthonormée.
Pour le vecteur \(\overrightarrow{OA}\) représenté en figure 5, on peut attribuer une coordonnée selon l'axe des \(x\) et une autre coordonnée selon l'axe des \(y\). Ces coordonnées du vecteur peuvent s'exprimer à partir des coordonnées \((x_O, y_O)\) et \((x_A, y_A)\) des points \(O\) et \(A\). On notera au choix : $$\boxed{\overrightarrow{OA} (x_A-x_O,y_A-y_O)\ \textrm{ ou }\ \overrightarrow{OA} \begin{pmatrix}x_A-x_O\\y_A-y_O\end{pmatrix}\ \textrm{ ou }\ \overrightarrow{OA}=(x_A-x_O) \ \overrightarrow{i}+(y_A-y_O)\ \overrightarrow{j}}$$
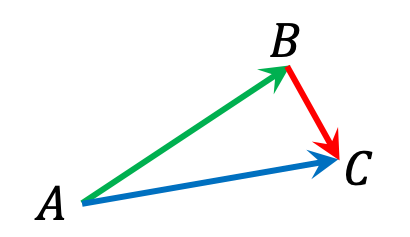
Il est possible d'additionner deux vecteurs. Il est utile de rappeler pour cela la relation de Chasles : $$\Large \boxed{\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}}$$
2. Étude d'une trajectoire
2.1. Définition
Une trajectoire est l'ensemble des positions successives prises par le système au cours du temps.
Il est possible d'étudier les différents types de trajectoires que peut décrire un système. On peut alors les regrouper en trois catégories :
- Les trajectoires rectilignes décrivent des droites.
- Les trajectoires circulaires décrivent des cercles.
- Les trajectoires curvilignes décrivent tout autre type de trajectoire.
 |
 |
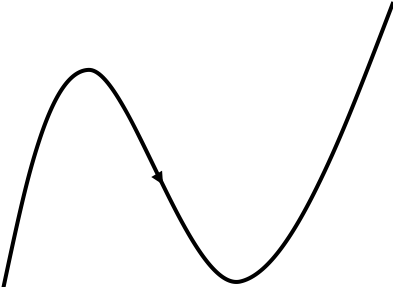 |
| (a) Trajectoire rectiligne | (b) Trajectoire circulaire | (c) Trajectoire curviligne |
Une étude de l'évolution de la vitesse au cours du mouvement peut être également réalisée. On peut également classer les mouvements en trois catégories :
- Les mouvements dont la vitesse diminue sont dits "décélérés".
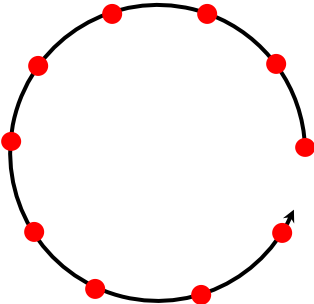
- Les mouvements dont la vitesse est constante sont dits "uniformes".
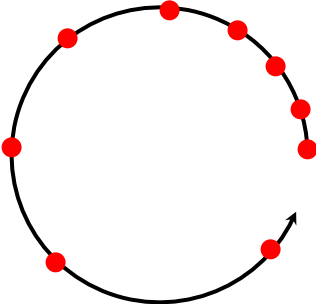
- Les mouvements dont la vitesse augmente sont dits "accélérés".
Il est ainsi possible de répartir les différents mouvements suivant neuf catégories représentées dans la figure ci-dessous.
| Mouvement | Décéléré | Uniforme | Accéléré |
|---|---|---|---|
| Trajectoire rectiligne |  |
 |
 |
| Trajectoire circulaire | 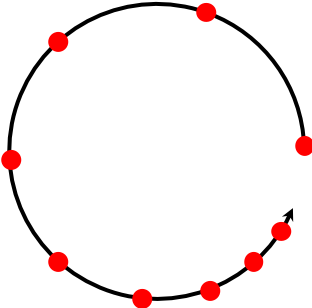 |
 |
 |
| Trajectoire curviligne |  |
 |
 |
2.2. Position d'un point
le vecteur position \(\overrightarrow{OM}\) part de l'origine \(O\) du repère et va jusqu'au point \(M\), position instantannée du système ponctuel.
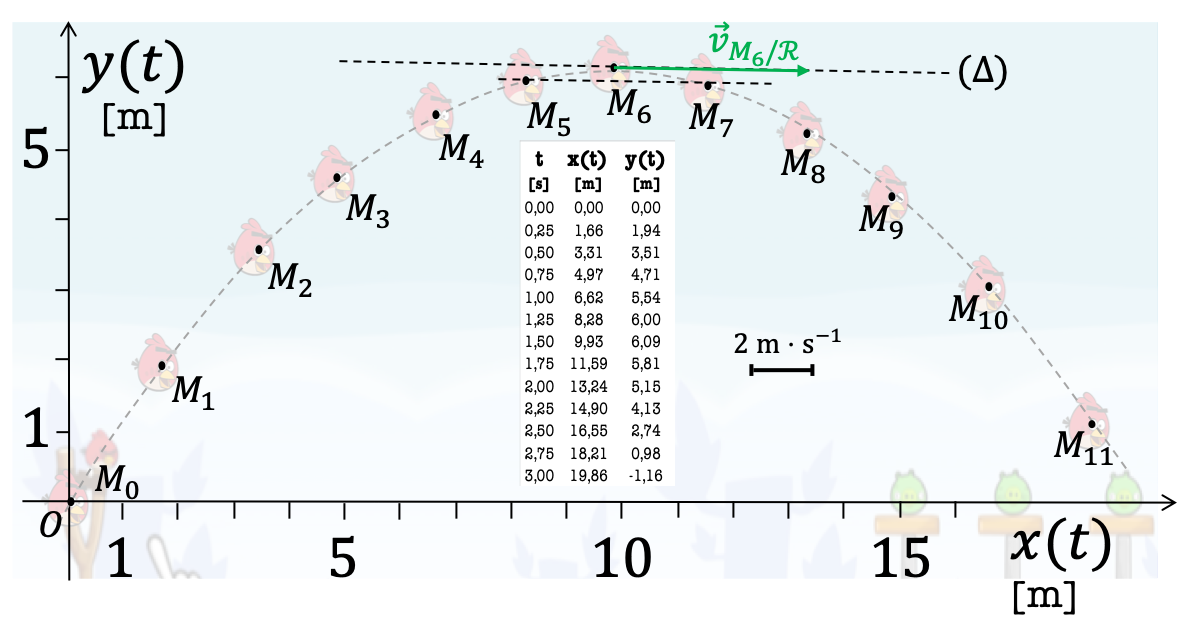
La figure suivante représente la trajectoire de Red dans le jeu Angry Birds®. Ses positions successives toutes les \(\Delta t=0,25 \ \mathrm{s}\) sont repérées par les points \(M_0\), \(M_1\), etc. Ce type de représentation s'appelle une chronophotographie.
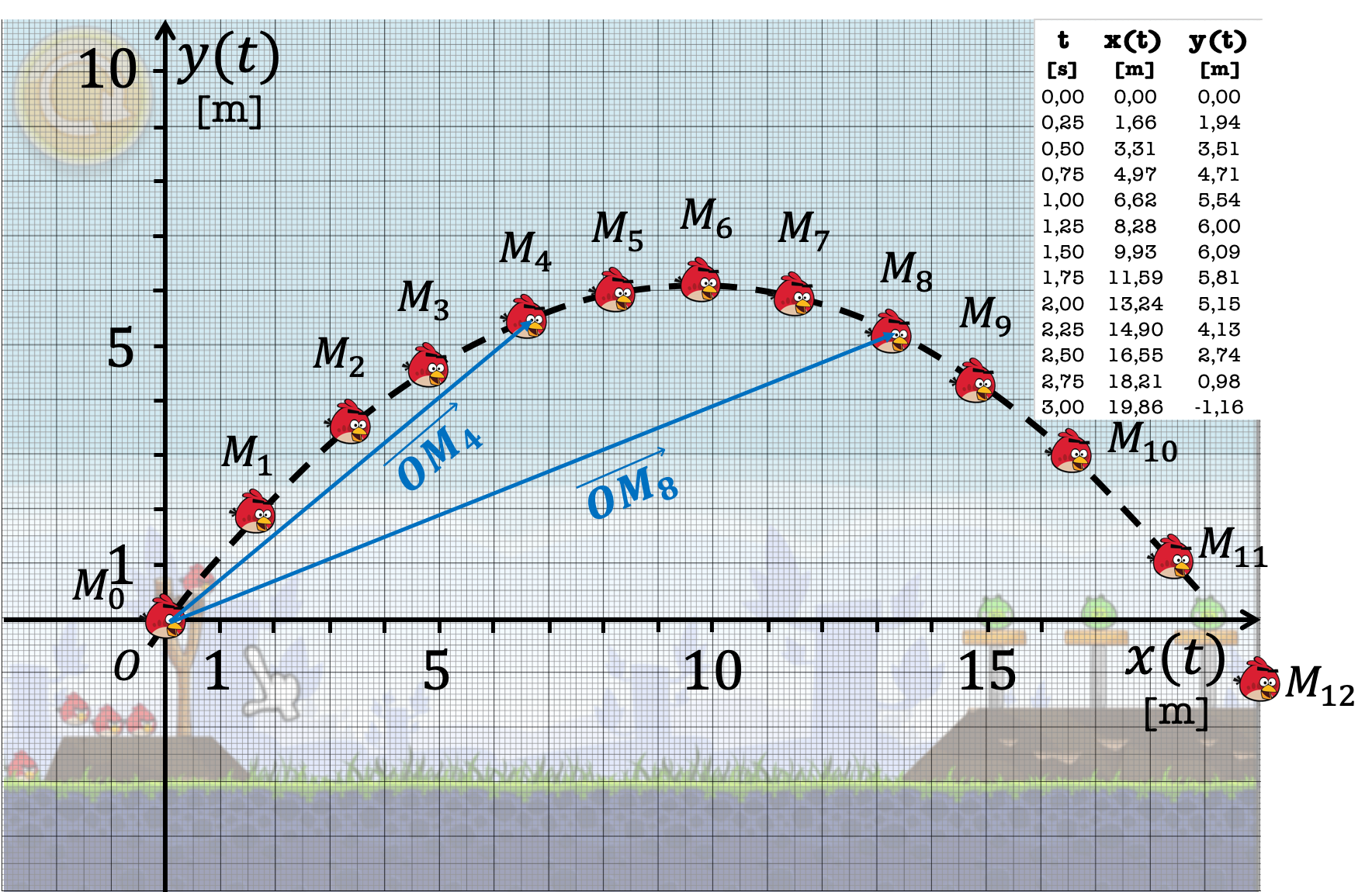
Figure 9 : Chronophotographie du mouvement curviligne de Red.
2.3. Vitesse d'un point
Le vecteur vitesse \(\overrightarrow{v}_{M, \mathcal{R}}\) d'un système en mouvement dans le référentiel \(\mathcal{R}\) entre les points \(M\) et \(M'\) est défini à partir du vecteur déplacement \(\overrightarrow{MM'}\) par : $$\Large \boxed{\overrightarrow{v}_{M, \mathcal{R}}=\frac{\overrightarrow{MM'}}{\Delta t}}$$ où \(\Delta t\) est la durée mise par l'objet pour aller de \(M\) à \(M'\).
La représentation d'un vecteur vitesse sur différentes positions d'une chronophotographie doit vérifier certaines étapes nécessaires pour être bien tracée. Deux cas peuvent se présenter :
-
Le vecteur vitesse est tracé de façon graphique.
Dans ce cas, toutes les positions \(M_0\), \(M_1\), etc sont généralement représentées. On notera "i" l'indice de la position que l'on étudie de sorte que \(\overrightarrow{OM_i}\) soit le vecteur position et \(\overrightarrow{v}_{M_i, \mathcal{R}}\) le vecteur vitesse au point \(M_i\). Les étapes à suivre pour tracer le vecteur vitesse \(\overrightarrow{v}_{M_i, \mathcal{R}}\) sont donc les suivantes :- Tracer la droite \((\Delta)\) parallèle à \((M_{i-1}M_{i+1})\) passant par \(M_i\).
- Calculer la norme du vecteur vitesse \(v=\left|\left|\overrightarrow{v}_{M_i, \mathcal{R}}\right|\right| =\left|\left|\frac{\overrightarrow{M_{i-1}M_{i+1}}}{2 \Delta t}\right|\right| \).
- Calculer la longueur du vecteur vitesse à l'aide d'une échelle de représentation.
- Tracer le vecteur vitesse en partant du point \(M_i\), selon la droite \((\Delta)\) et orienté dans le sens du mouvement.
- Nommer \(\overrightarrow{v}_{M_i, \mathcal{R}}\) le vecteur ainsi représenté.
-
Le vecteur vitesse est tracé de façon numérique.
Dans ce cas, il est généralement nécessaire de connaître les vecteurs position \(\overrightarrow{OM_i}\) et vitesse \(\overrightarrow{v}_{M_i, \mathcal{R}}\) pour pouvoir en déduire la position suivante \(M_{i+1}\) du système. On a donc à disposition, uniquement les positions \(M_i\) et \(M_{i-1}\). Les étapes à suivre pour pouvoir représenter le vecteur vitesse de façon numérique sont donc les suivantes :- Déclarer les variables \(v_x\) et \(v_y\) qui représentent les coordonnées du vecteur vitesse selon les axes \(Ox\) et \(Oy\).
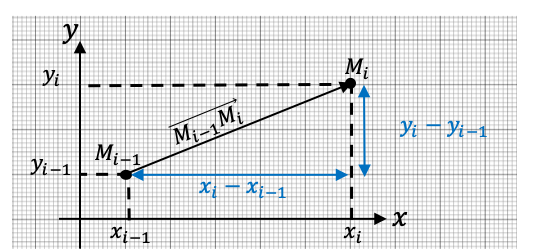
- Déclarer les variables \(x_i\) et \(y_i\) puis \(x_{i-1}\) et \(y_{i-1}\) qui représentent les coordonnées respectives des points \(M_{i-1}\) et \(M_{i}\).
- Réaliser les affectations suivantes : \(v_x=\frac{x_i-x_{i-1}}{2 \Delta t}\) et \(v_y=\frac{y_i-y_{i-1}}{2 \Delta t}\).
- La représentation du vecteur vitesse dépend de la syntaxe du langage de programmation utilisé.
Comme pour tout vecteur, il est possible de calculer la norme du vecteur vitesse à partir de ses coordonnées. On note les deux vecteurs position successifs par \(\overrightarrow{OM}(x_M,y_M)\) et \(\overrightarrow{OM'}(x_{M'},y_{M'})\). Le vecteur déplacement s'écrit donc \(\overrightarrow{MM'}(x_{M'}-x_M,y_{M'}-y_M)\). Par conséquent le vecteur vitesse s'écrit \(\overrightarrow{v}_{M, \mathcal{R}} \begin{pmatrix} \frac{x_{M'}-x_{M}}{2 \Delta t}\\ \frac{y_{M'}-y_{M}}{2 \Delta t} \end{pmatrix}\). La norme de ce vecteur s'écrit donc : $$\large \boxed{\left|\left|\overrightarrow{v}_{M, \mathcal{R}}\right|\right|=\frac{1}{2 \Delta t} \sqrt{(x_{M'}-x_M)^2 + (y_{M'}-y_{M})^2}}$$