GÉNÉRAL

PHYSIQUE

CHIMIE

Introduction à l'électrocinétique

Différentes branches de la physique étudient les phénomènes liés à l'électricité :

L'électrocinétique est la science qui étudie les lois de comportement des circuits électriques et du déplacement de l'électricité dans les milieux matériels.
L'électrostatique, par opposition à l'électrocinétique, étudie les phénomènes créés par des charges électriques statiques par rapport à un observateur.
L'électronique utilise les lois de l'électrocinétique à des fins de traitement, de transmission ou de stockage d'informations.
L'électrotechnique désigne l'étude des applications techniques de l'électricité : production dans des centrales, transport, distribution, conversion, etc.

L'objectif de ce cours est d'apporter les premiers éléments de compréhension sur l'électricité ainsi que d'introduire les grandeurs physiques qui seront utilisées plus tard pour faire une modélisation mathématique d'un circuit électrique.

1. Qu'est-ce que l'électricité

1.1. Approche historique

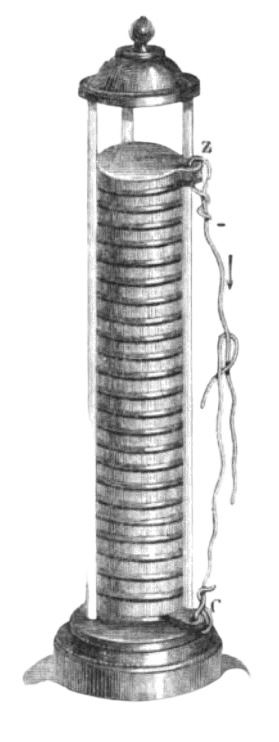
Le phénomène est connu depuis l'antiquité (on doit d'ailleurs le mot électricité au mot grec êlektron ($ \eta \lambda \varepsilon \kappa \tau \rho o \nu$ ) mais on peut dater un tournant essentiel à son essor en $1799$ lorsque l'Italien Alessandro Volta met au point la première " pile voltaïque" en empilant alternativement des disques de zinc et de cuivre séparés par un disque de feutre imbibé d'acide. Cette invention lui vaudra le titre de comte du Royaume décerné par l'Empereur des Français, Napoléon Bonaparte. Le Français André-Marie Ampère met au point la première machine de mesure de l'intensité d'un courant électrique en $1821$ et invente le terme de " tension électrique"".


(a) André Marie Ampère	(b) Pile voltaïque de A. Volta	(c) Alessandro Volta

Figure 1 : Les premiers pas de l'électrocinétique

Les applications liées à l'utilisation de l'électricité sont légion, mais on peut résumer l'intérêt ce cette découverte par une citation de Michael Faraday. Lorsque le Chancelier de l’Échiquier britannique William Gladstone a demandé à Michael Faraday à quoi pourraient bien servir ses recherches sur l’électricité, le célèbre scientifique du XIX $^\textrm{ème}$ siècle lui a répondu : « Un jour, cher monsieur, vous pourrez la taxer ! ».

Figure 2 : Palais de l'électricité à l'Exposition universelle de Paris en $1900$

La "fée électricité" permet le développement d'un nombre colossal de nouvelles technologies qui révolutionnent la vie quotidienne. Parmi elles, le moteur à courant continu inventé par Michael Faraday ( $ 1821$), le télégraphe électrique ($1838$) mis au point par le Britannique Charles Wheatstone entre Londres et Birmingham, l'ampoule électrique conçue par l'Américain Thomas Edisson ($1879$), le moteur synchrone de Nikola Tesla ($1888$) ou encore le cinématographe inventé par les frères Lumière ($ 1895$).

1.2. Un déplacement de porteurs de charge(s)

L'électricité est liée à un déplacement de porteurs de charges électriques sous l'effet de ce que l'on appelle une différence de " potentiels électriques".

Pour comprendre la nature des porteurs de charge, il est nécessaire de revenir à la structure de la matière et à celle de l'atome. Un atome, entité infinitésimale composant la matière qui nous entoure, est composé :

de protons, particules massives ( $m=1,67 \times 10^{27} $ kg) pour une taille de l'ordre de $10^{-15} \mathrm{m} = 1 $ fm qui composent le noyau de l'atome. Ces particules portent une charge électrique $+e=+1,6 \times 10^{-19} $ C.
de neutrons, approximativement de même masse et de même taille que les protons, mais non chargés électriquement.
d'électrons, particules élémentaires $1835$ fois plus légères qu'un proton ($m=9,1 \times 10^{-31}$ kg) et de charge électrique $-e=-1,6 \times 10^{-19}$ C.

On désigne par "nucléon" les termes de proton et de neutron.

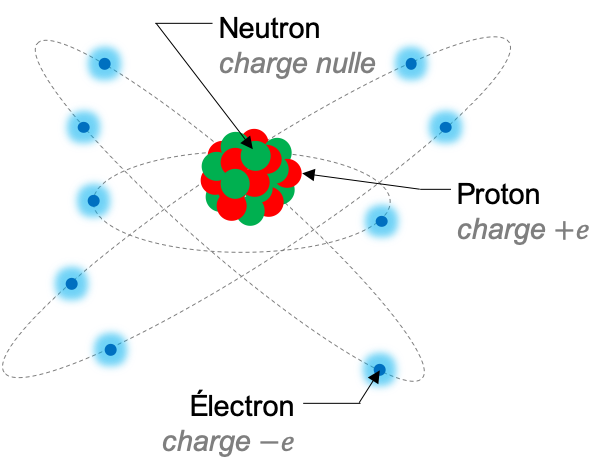
La structure d'un atome est électriquement neutre, c'est-à-dire qu'il y a obligatoirement le même nombre de protons (de charge $+e$) que d'électrons (de charge $-e$).

Un porteur de charge peut être de deux natures : il s'agit soit d'un électron, soit d'un ion (atome auquel on a arraché ou ajouté un ou plusieurs électrons et qui acquiert une charge électrique globale non nulle).

Un métal peut être vu comme une suite agencée (structure cristalline) d'atomes. Les noyaux des atomes ainsi que les électrons les plus proches du noyau (électrons de coeur) n'ont pas de mouvement d'ensemble : ils oscillent autour d'une position fixe. En revanche, les électrons les plus éloignés du noyau (électrons de conduction) peuvent être mis en commun avec d'autres atomes dans une mer d'électrons. Un métal n'est en fin de compte ni plus ni moins qu'un réseau de cations (ions chargés positivement) collés entre eux par une mer d'électrons. Cette constitution est donc propice au déplacement des électrons dans tout le métal, contribuant ainsi à la conduction d'un courant électrique.
Il existe d'autres milieux conducteurs comme les solutions ioniques. Dans ce cas, le porteur de charge sera un ion. Contrairement à l'électron qui est toujours chargé d'une charge $-e=-1,6\times 10^{-19} $ C, un ion peut avoir une charge multiple $-e,-2e,-3e,\ldots$, on parle alors d'anion, ou $+e,+2e,+3e,\ldots$, on parle dans ce cas de cation.

Exemple :

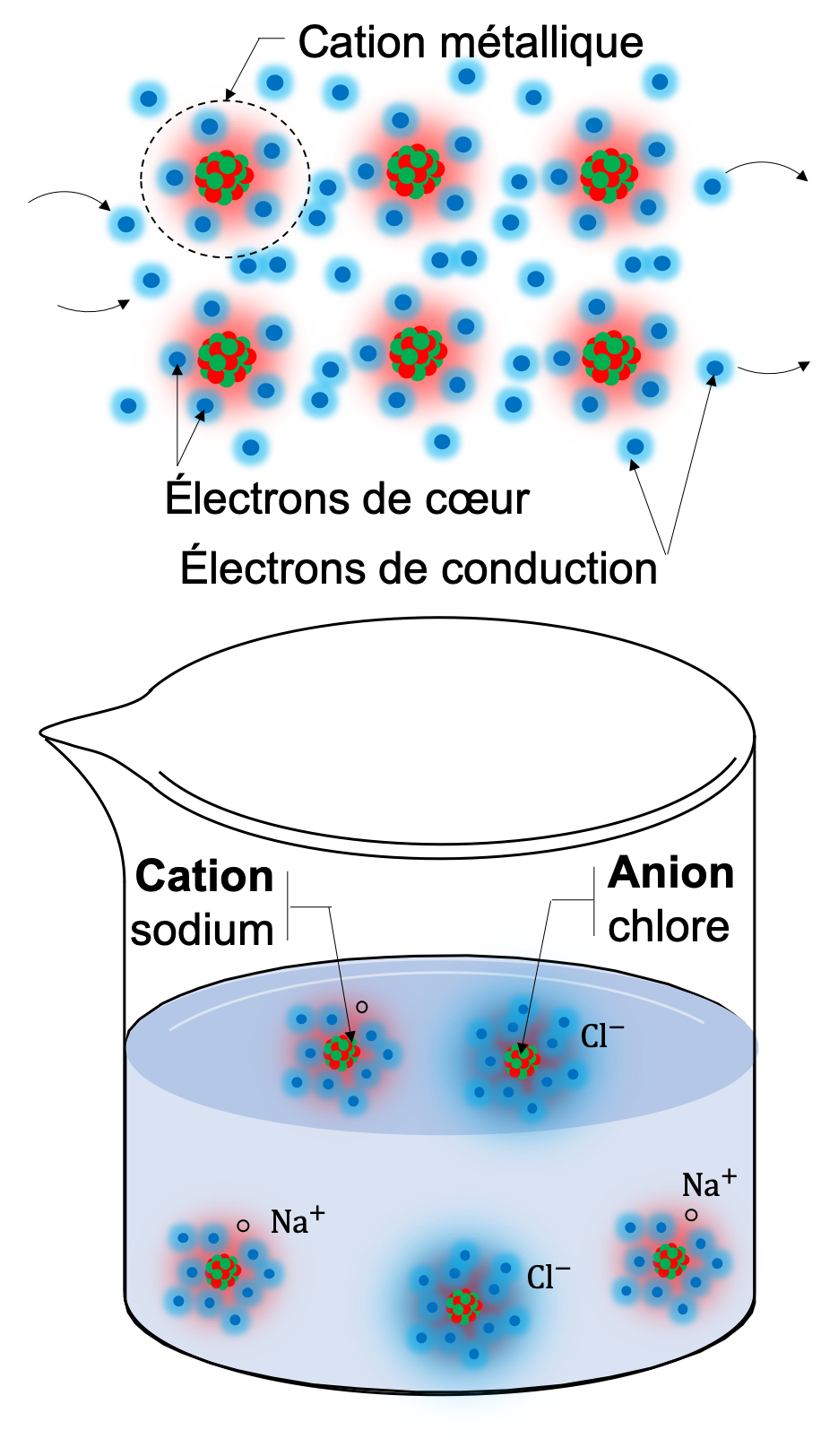
Du sel de table (de formule $ \mathrm{Na,Cl_{(s)}}$) se dissout dans l'eau en formant des cations sodium $\mathrm{Na^+}$ (charge $+e$) et des anions chlore $\mathrm{Cl^-}$ (charge $-e$). L'eau salée est donc un milieu conducteur d'électricité.

1.3. Les grandeurs électrocinétiques

On peut définir deux grandeurs pour caractériser les propriétés d'un courant électrique. La tension électrique et l'intensité du courant électrique.

Définition : Tension électrique $ U $
La tension électrique, notée $U$ (ou $U_{AB}$) est égale à la différence de potentiel entre deux bornes $A$ et $B$ d'un circuit : $U_{AB}=V_A-V_B$. Elle se représente avec une flèche qui pointe vers le potentiel $V_A$ à la borne $A$.

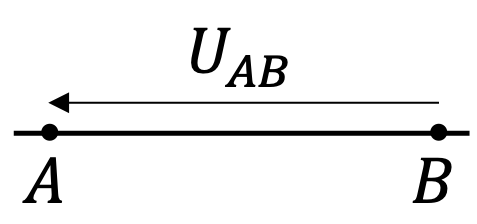Figure 3 : Représentation de la tension entre les bornes $A$ et $B$.

L'unité d'une tension est le Volt (V) en hommage à A. Volta. Dans le système d'unités international, on a la décomposition suivante $1$ V $= 1\ \mathrm{kg.m^2.s^{-3}.A^{-1}}$.
Exemple :
- Une pile du commerce délivre une tension de $1,5$ V
- La tension aux bornes d'une prise en Europe est de $230$ V, $110$ V en Amérique du Nord.
- La tension dans le réseau de transport d'électricité de RTE est de $400 $ kV (HTA) et $225 $ kV (HTB).

Définition : Intensité du courant électrique $ I $

L'intensité $I$ du courant électrique est le nombre de charges $ \Delta q$ qui traversent une portion de circuit en un instant $ \Delta t$. On note alors $$I=\frac{\Delta q}{\Delta t}$$ On représente l'intensité $I$ du courant électrique dans un fil conducteur à l'aide d'une flèche.

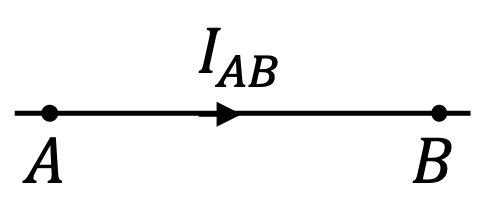Figure 4 : Représentation de l'intensité $I$ du courant qui traverse un fil conducteur.

L'unité de l'intensité du courant électrique est l'Ampère (A), en hommage au Français A.M. Ampère. C'est l'une des sept unités de base du système international d'unités.

Exemple :

L'intensité du courant dans un circuit électronique est de l'ordre du microampère ($\mathrm{\mu A}$) ou du milliampère ($\mathrm{mA}$)
L'intensité maximale qui sort d'une prise électrique en Europe est $16$ A

Notons dès à présent que la flèche qui permet de représenter la tension $U_{AB}$ entre les bornes $A$ et $B$ est opposée à la flèche qui représente l'intensité $I_{AB}$ qui traverse le circuit de la borne $A$ vers la borne $B$.

Pour comprendre la signification d'un potentiel électrique ou d'une tension électrique, on peut raisonner par analogie avec un support incliné sur lequel circulent des billes.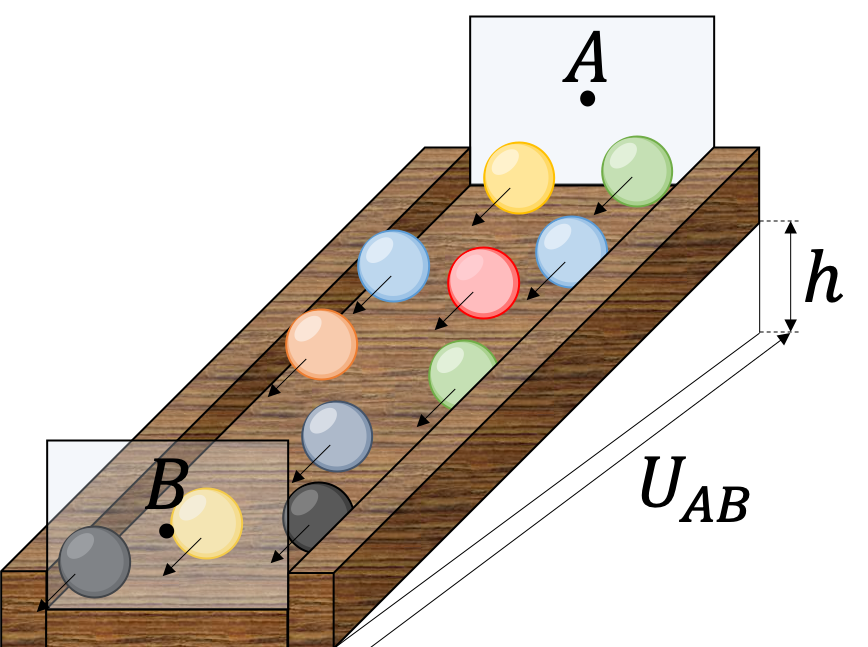

Figure 5 : Analogie mécanique de la tension et de l'intensité du courant électrique.

On peut donc dresser la tableau d'analogie suivant :

Circuit électrique	Circuit de billes
Fil conducteur (réseau de cations et électrons de cœur)	Rampe en bois
Électron de conduction	Bille
Tension électrique $U_{AB}$ (différence de potentiels électrique)	Dénivelé $h$ (différence d'altitude)
Intensité $I$ du courant électrique	Nombre $N$ de billes qui traversent la surface bleue au niveau du point $A$ dans un intervalle de temps $\Delta t$.

Table 1.1 - Analogie entre un circuit électrique et un circuit de billes

Attention : En régime stationnaire, les électrons se déplacent dans le sens des potentiels croissants (dans le sens de la flèche de la tension). Comme ils portent une charge négative $-e$, l'intensité du courant est bien comptée positive lorsque les flèches de la tension et de l'intensité s'opposent. Il s'agit là d'une limite à l'analogie entre le circuit électrique et le circuit de billes.

La vitesse des électrons est relativement faible, de l'ordre du centimètre par heure (en fonction de l'intensité du courant), en revanche l'onde qui se propage pour transmettre le mouvement aux électrons est très rapide, de l'ordre de $10^8\ \mathrm{m \cdot s^{-1}}$. Quand on branche un appareil électrique, tous les électrons sont donc mis en mouvement quasi instantanément.

2. Les lois de l'électrocinétique

2.1. Définitions

Pour représenter schématiquement un fil électrique, on utilise un simple trait.

Tous les autres composants électriques possèdent leur propre symbole.

Interrupteur	Conducteur ohmique	Pile	LED	Moteur à courant continu

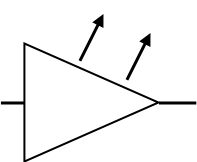
Table 1.2 - Représentation schématique de certains composants électriques

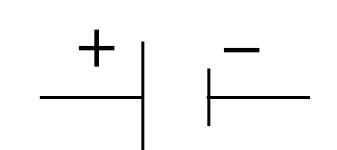
Définition : Noeud
Un nœud est le point de concours d'au moins $3$ branches.

Les nœuds sont généralement repérés sur un schéma par des lettres capitales (A,B,C,...)
Définition : Branche
Une branche est une portion de circuit électrique délimitée par deux nœuds.
- La branche qui contient le générateur (de tension, de courant, pile, etc) est appelée branche principale.
- Les autres branches (appelées branches dérivées ou secondaires) ne contiennent que des récepteurs.
Deux branches qui partagent les même nœuds sont montées en parallèle.

Dans une branche, l'intensité du courant est uniforme.
Définition : Maille
Une maille est un chemin fermé dans un circuit électrique.
Exemple :
- Le circuit ci-contre contient $3$ branches. Celle de gauche, comprenant le générateur de tension est la branche principale, les deux autres branches sont des branches dérivées.
- Les noeuds sont repérés par les lettres $A$ et $B$.
- Il y a $2$ mailles indépendantes repérées par les chiffres $ \mathrm{I} $ et $ \mathrm{II}$.
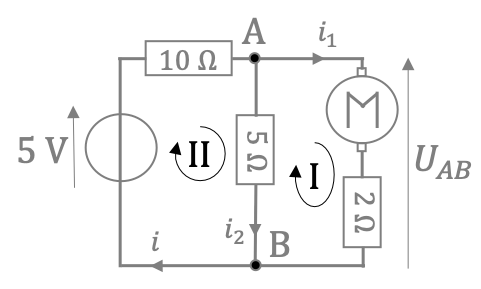Les trois branches sont en parallèle puisqu'elles partagent toutes les trois les mêmes nœuds (A et B).

La tension aux bornes des trois branches est donc commune et vaut $U_{AB}$. On retiendra que la tension aux bornes de deux branches montées en parallèle est identique.

Le moteur et la résistance de $2\ \Omega$ sont montés en série.

La résistance de $2\ \Omega $ et celle de $5\ \Omega$ ne sont montées ni en série, ni en parallèle.

On repère les intensités $i$, $i_1$, $i_2$ des courants qui traversent chaque branche. L'intensité du courant dans une branche étant unique, l'intensité du courant qui traverse la résistance de $2\ \Omega$ et celle qui traverse le moteur sont identiques : il s'agit de $i_1$.

2.2. Les lois de Kirchhoff

Les lois de Kirchhoff sont des propriétés physiques qui s'appliquent sur les circuits électriques. Ces lois portent le nom du physicien allemand Gustav Kirchhoff (ci-contre) qui les a établies en 1845. Les deux lois de Kirchhoff sont :

La loi des noeuds

La loi des nœuds précise que "la somme algébrique des intensités des courants qui entrent par un nœud est égale à la somme algébrique des intensités des courants qui en sortent".

La loi des mailles

La loi des mailles stipule que "dans une maille d'un réseau électrique, la somme des tensions le long de cette maille est toujours nulle".

Exemple :

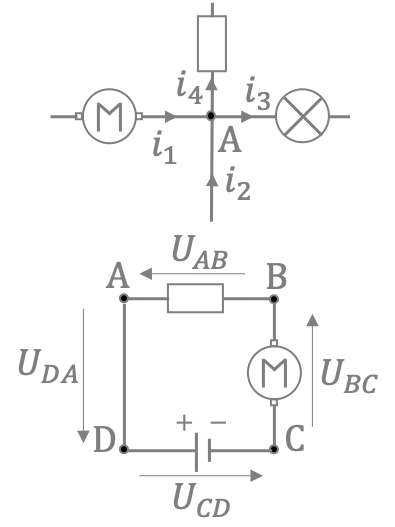
En considérant le nœud $A$ ci-contre, la loi des noeuds permet de préciser que la somme des intensités des courants arrivant vers le nœud est égale à la somme des intensités des courants qui en repartent. On a donc la relation suivante : $$i_1+i_2=i_3+i_4 \Leftrightarrow i_1+i_2-i_3-i_4=0$$
En considérant la maille suivante, la loi des mailles permet de préciser que la somme des tensions orientées est nulle, soit : $$U_{AB}+U_{BC}+U_{CD}+U_{DA}=0$$

La tension aux bornes d'un fil est toujours nulle, soit $U_{DA}=0$ V.

Comme il n'y a qu'une maille (pas de nœuds), l'intensité du courant est la même dans chaque branche de la maille.

3. Mesurer une tension ou une intensité électrique

3.1. Le multimètre

Le multimètre est un appareil de mesure qui comporte entre autres un capteur de tensions électriques, appelé voltmètre et un capteur d'intensités de courants électriques, appelé ampèremètre. Le multimètre se présente de la façon suivante :

Figure 6 : Multimètre

Les branchements au circuit électrique dépendent de ce que l'on cherche à mesurer :

Pour mesurer une tension, brancher le premier câble électrique à la borne " V $\Omega$ " et le deuxième câble à la borne "COM". Sélectionner ensuite le calibre souhaité ( $\mathrm{\tilde{V}}$, $ \mathrm{\overline{\dddot{V}}}$, $ \mathrm{m\overline{\dddot{V}}}$).
Pour mesurer une intensité, brancher le premier câble sur le calibre sélectionné ($\mathrm{A}$, $\mathrm{mA}$) et le deuxième sur la borne "COM".

3.2. Le voltmètre

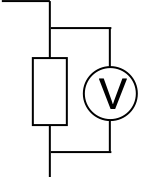
Pour brancher un voltmètre aux bornes d'un dipôle (générateur, conducteur ohmique, LED, ampoule, moteur, etc), il faut relier la borne "V $\Omega$" et la borne "COM" à chaque borne du dipôle. De fait, le dipôle et le voltmètre sont branchés en parallèle.

3.3. L'ampèremètre

Pour brancher un ampèremètre dans une branche, il faut insérer l'ampèremètre en série avec les autres dipôles, en reliant la borne "$\mathrm{A}$" ou "$\mathrm{mA}$" d'un côté et la borne "COM" de l'autre.

Les représentations schématiques des branchements du voltmètre et de l'ampèremètre sont les suivantes :


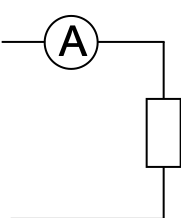(a) Branchement d'un voltmètre aux bornes d'un conducteur ohmique	(b) Branchement d'un ampèremètre en série avec un conducteur ohmique

Figure 7 : Les branchements d'un multimètre